To the ancient Greek, Urania was the Muse of the Heavens and Uranus was the god of the celestial realm. The planet Uranus, that was discovered in 1781 by the English astronomer William Herschel, was named after him. Both names, Urania and Uranus, come from the Greek root for sky, urano. The word uranography is derived from that same word, and refers to celestial cartography, just like geography refers to terrestrial mapping.
The Oldest Star Maps
Beyond a doubt, the bright night sky has always made a great impression, and the ancient peoples let their fantasies run wild: in the star patterns they recognized bears, dogs, and hunters. These star groupings became known as constellations, and many of these old constellations are still known today, e.g., the Great Bear, the Lion, the Charioteer, the Scorpion, and the Herdsman.
The oldest attempts to map the sky date from the second millenium, before Christ. On boundary stones found in the ruins of the ancient city of Babylon, drawings of some of these classical constallations were found. In those days, and long after, astronomy and astrology were connected, and regarded the same science. The most important task of an astrologer was to predict the future by looking at the positions of the stars, and especially the planets. Today, if you want to insult an astronomer, you call him an astrologer. Astrology is regarded a pseudoscience. The twelve constellations of the zodiac that we know from the astrology columns in papers and magazines, date from the time of Babylon.
Later, in Classical Greek times, many of the old constellations received new names derived from the many gods and semigods in Greek mythology. Orion, Cassiopeia, Cepheus, Andromeda, and Hercules, just to name a few, have survived the centuries, and can still be found on modern star charts.
One of the earliest uranographical works that has been saved is the Almagest, of the second century A.D. by the Greek astronomer Claudius Ptolemaeus (Ptolemy). The work contained, amongst others, a list of 48 constellations that were recognized in his time and in his part of the world. These 48 constellations are still recognized today, with just two exceptions. The name Serpentarius (Serpent Holder) has been changed to the personal name Ophiuchus, and the name Argo (or Argo Navis) does not exist anymore, because the large constellation, the ship Argo, is now devided into three parts: the Stern (Puppis), the Keel (Carina), and the Sails (Vela).
The Almagest also contains a list of 1,022 stars measured with an exceptional accuracy for those days. The positions are given in ecliptic coordinates, because the Ecliptic was, due to the importance of astrology, the most important line in the sky. But the star positions were also given in a quite different way. In his listing of stars in the Great Bear, you read things like: “The star at the tip of the muzzle”, “The western star of those in the two eyes” or “The western star of the two in the forehead”. This meant that people using that list needed to be familar with the anatomy of those heavenly figures.
On many medieval maps the stars seem to be less important than the figures; the correct positioning of the stars was not the first priority. Moreover, on some of these old maps the stars are completely absent (see figure 1).

Figure 1. Star map by Giovanni Cinico (Napels, 1469). Notice that there are no stars shown, only the constellation figures.
In Ptolomy’s catalog stars were divided into six classes of brightness, or magnitudes. The brightest stars were called first magnitude, the less bright stars second magnitude and so on. The faintest stars, still visible to the naked eye, were called magnitude six.
This rather rough magnitude scale was refined later on a scientific (logarithmic) scale by the English astronomer Norman Pogson. He defined that a star of magnitude 1 was exactly 100 times as bright as a star of magnitude 6. This means that a difference of 1 magnitude represents a difference in brightness of 2,5119 (the 5th power root of 100). Based on this logarithmic scale the brightness of stars are now given with more accuracy, with one or two decimals. For instance, Regulus is a star of magnitude 1.39. On this new scale some stars turned out to be brighter than magnitude 1 and the scale was expanded to 0, but some stars were even brighter than that. These stars have a negative magnitude: Arcturus (-0.05), Rigil Kentaurus (-0.27), Canopus (-0.74), and Sirius (-1.46).
Obviously, the scale can be extended in both directions. Our sun, by far the brightest object in the sky, has a magnitude of -26.74. On the other end of the scale we see that the faintest stars to be captured on photographs by the the big ground-based telescopes are of approximately magnitude 27. Hubble’s Space Telescope has even captured stars of magnitude 31 on long exposed images.
New Constellations
In 1515 Alrecht Dürer published the first printed maps; a pair of woodcut maps showing the northern and southern hemisphere (figure 2). The maps show the 48 classical constellations, listed by Claudius Ptolemaeus (Ptolemy) in the 2nd century. A large area of the southern sky is still void of constellations. In the western world this part of the sky was yet unexplored. Between 1595 and 1597, two Dutchmen: Pieter Keyser and Cornelis de Houtman observed the southern sky on their first expedition to the Far East, commisioned by a scientist from Amsterdam, Peter Plancius. A star list, along with twelve new constellations, was created.

Figure 2. Northern and southern hemisphere on a pair of woodcut maps from Albrecht Dürer (Neurenberg, 1515).
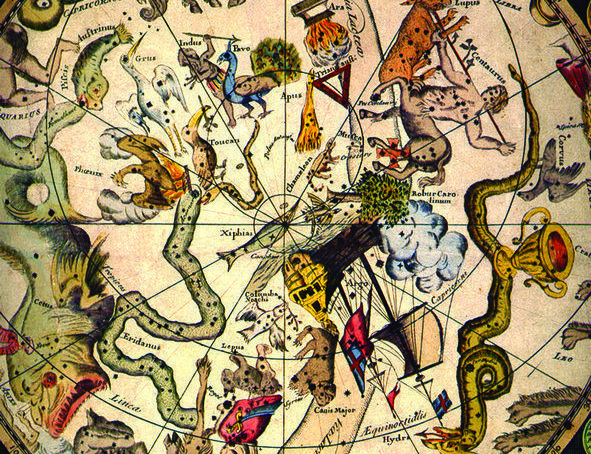
Some believe that Keyser and De Houtman invented the constellations, but others say that Peter Plancius was the spiritual father. Peter Plancius was a bird-lover and among those new constellations we find five birds: the Phoenix, the Crane, the Tucan, the Peacock, and the Bird of Paradise (figure 3). Later, in 1752, the French Astronomer Nicolas Louis de Lacaille made more additions to the southern sky, by creating a number of “modern” constellations. So today we have a Telescope, a Microscope, an Octant, a Pendulum Clock, and an Airpump, alongside the classical figures.
Figure 3. New constellations in the southern sky, pictured on a map by James Barlow (London, 1790).
The period between 1600 and 1800 was a turbulant time for the starry sky. Constellations came and went. Almost everyone who created star maps invented new constellations, sometimes to fill empty spaces, but more frequently parts of existing constellations were simply amputated to make room for their own inventions. Very often this was done for political reasons, or in other words to get in good graces with prominent people, like kings and emperors. A nice example is The Scepter and the Hand of Justice on a map from 1679 by Augustin Royer, an architect at the French Court. It was dedicated to the emperor, Louis XIV of France. It is in the area were we now find Lacerta, The Lizard (figure 4). It will be clear that these new inventions usually did not have a long life!
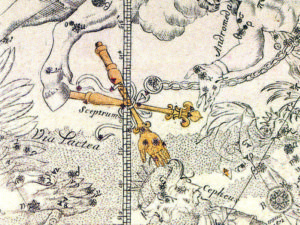
Figure 4. “The Scepter and the Hand of Justice” on a map by Augustin Royer (Paris, 1679). The constellation was dedicated to Emperor Louis XIV.
Some Major Star Atlases
In 1603 Johannes (Johann) Bayer, a lawyer from Augsburg in Germany published a milestone in stellar cartography, his Uranometria. Bayer’s atlas contains 48 star maps, each showing one of the 48 classical constellations from Ptolemy’s list, plus one map showing the twelve newly created southern constellations. Bayer was the first to use Greek letters to identify the stars in a constellation. Since the publication of his Uranometria, Betelgeuse in the constellation of Orion is also known as α (alpha) Orionis and Rigel as β (beta) Orionis. It is a general misconception that he always asigned the first letter of the Greek alphabet (α) to the brightest star. There are many obvious examples where Bayer probably used different criteria in deciding about the letter sequence.
The seven stars of the Big Dipper (part of The Great Bear) have been given Greek letters (α, β, γ, δ, ε, ζ and η) in the order that they appear in the dipper, from right to left, disregarding the differences in brightness. Another example is Sagittarius, where the letters α and β are assigned to Rukbat and Arkab, both 4th magnitude stars in the most southern part of the constellation. In spite of all arguments about this, it is interesting to see that on Bayer’s map of Sagittarius, these two rather faint stars are shown as being the brightest stars in the constellation. (figure 5).
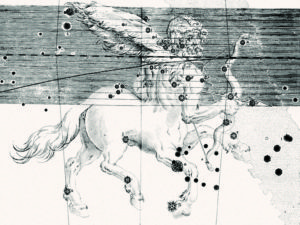
Figure 5. The constellation of Sagittarius, as shown in Uranometria, by Johannes Bayer (Augsburg, 1603). Note that the two faint stars α and β, in the front right leg, are shown as the brightest stars in the constellation, while they both are rather faint (magnitude 4).
A very interesting and beautiful atlas was published in 1627, by Julius Schiller, a Roman Catholic lawyer, also from Augsburg in Germany: Coelum Stellatum Christianum (The Christian Sky). All the pagan gods and godesses are removed, together with almost all the other classical figures, their places taken by new constellations, based on figures from the Bible and the Christian tradition. The twelve constellations of the Zodiac are now the twelve apostles. The sky north of the ecliptic is dedicated to the New Testament, while south of ecliptic only figures from the Old Testament are shown. The large constellation Argo (or Argo Navis) was renamed a few decades earlier by Peter Plancius, who called it Arca Nöe (Noah’s Ark), and Plancius also created a new constellation close to it, Columba (The Dove, actually Noah’s Dove). These two constellations survived the cleanup by Schiller, together with one southern constellation from Ptolemy’s list: Ara (The Altar). The real beauty of this atlas can be seen in figure 6. The maps were true pieces of art, and although the idea of a Christian Sky gained some popularity, eventually the classical constellations prevailed.

Figure 6. The flying creature Pegasus, the winged horse, now changed to another flying creature, the angel Gabriël, in Coelum Stellatum Christianum, by Julius Schiller (Augsburg, 1629).
The next major star atlas to be published was Uranographia (or, if you prefer the complete title: Firmamentum Sobiescianum sive Uranographia), by Johannes (Johann) Hevelius. Published in 1687, this beautiful work almost equals the artistic quality of Schiller’s atlas. One peculiar thing about the atlas (like many others in those days) is that the maps show the sky mirror-reversed (figure 7), a strange phenomenon that originated in the use of sky globes.

Figure 7. Taurus, the Bull, as shown in Uranographia, by Johann Hevelius (Danzig, 1687). Notice that the sky is shown mirror-reversed.
On a globe of the Earth we see the Earth as it is, with features just as we would see it from space. But the sky can be regarded as a huge, imaginary sphere, with the observer inside. In other words, we look at the inside of that sphere, while a sky globe is viewed from the outside. So when a skyglobe was created, the stars and constellations were shown as they would appear from outside the imaginary sphere; that is, mirror-reversed. (figure 8).

Figure 8. Sky globe by Gerard Mercator (1551).
Without any reason that we can determine today, this mirror-reversed sky is also shown on many flat star maps, showing just a portion of the sky, like the ones in Uranographia. That mirror-reversed sky had some weird consequenses. Many stars were still referred to by the descriptions in Ptolemy’s catalog. Stars are described there as being in the right knee of Andromeda, or the in the left shoulder of Orion. On a mirror-reversed map, left becomes right and vise versa. To avoid confusion about left and right, many of the figures were turned around, so on these maps, you see the backsides of Andromeda, Orion, and many more. Looking at Auriga (the Charioteer), in Hevelius’ atlas, there is another remarkable thing: Auriga holds three goats to his breast, but since the Charioteeer was also turned around, the goats had to be moved to his back to prevent them from becoming invisible (figure 9).

Figure 9. Auriga, the Charioteer, as portrayed by Johann Hevelius in his Uranographia (Danzig, 1687).
The next landmark is Atlas Coelestis, published in 1729 by John Flamsteed, a British astronomer. It is one of the first atlases that used the equatorial coordinates and grid, while most older atlases used mainly the ecliptic coordinates. But the ecliptic grid is also shown, running at a slant (figure 10).

Figure 10. Ursa Major (The Great Bear) in Atlas Coelestis, by John Flamsteed (1729). Note the double coordinate grid.
The name Flamsteed is still well-known today, owing to the “Flamsteed” numbers—an alternate way of identifying the brighter stars inside a constellation. The numbers go in order of Right Ascencion, and many stars are referred to today by their Flamsteed number, e.g., 61 Cygni; star number 61 in the constellation of Cygnus. Many stars have both a Greek letter (assigned by Bayer) and a Flamsteed number. But here we have yet another misconception. Only Greek letters can be found on Flamsteed’s maps; no Flamsteed numbers. What happened is that in a French edition of the atlas and in the catalog, the editor, Joseph Jerome de Lalande, assigned these numbers to the stars in the catalog. So it was not Flamsteed who introduced the Flamsteed numbers, but Lalande!
One more star atlas to mention in this overview is again from a German astronomer, Johann Elert Bode. His Uranographia, published in 1801, was actually his second atlas. In 1782 he published an atlas with the title Vorstellung der Gestirne or Atlas Coelestis. It was a simplified version of Flamsteed’s atlas and also contained the catalog with those Flamsteed numbers. The only new thing to the atlas is the introduction of constellation boundaries, which are also shown in his second atlas, Uranographia. It set new limits. For the first time stars not visible to the naked eye are shown, and Bode uses chart projections that are far superior to everything done before. Bode uses mainly conical projections, and consequently, the atlas shows the stars and constellations with less destortion than most of its predecessors (figure 11). Bode’s Uranographia was an important step towards the more “modern” star atlases from the 19th and 20th centuries.
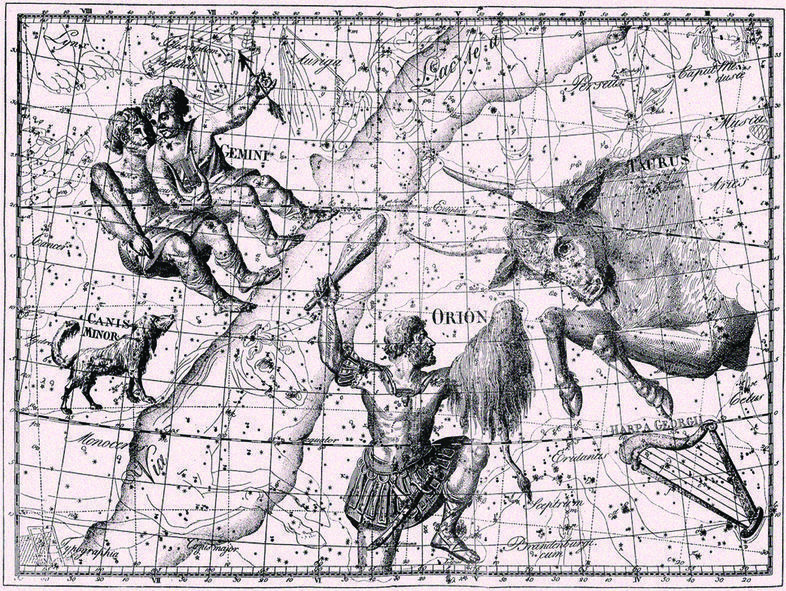
Figure 11. Orion, Taurus, Gemini and Canis Minor in Uranographia by John Elert Bode (1801). Bode uses properly constructed conic projections, which were far superior to the sinusoidal projection that was used on many earlier star charts.
The Transitional Phase
The German astronomer Friedrich Wilhelm Argelander published his Uranometria Nova in 1843. This atlas is often regarded as representing the transition from the classical to the modern star atlases. All naked-eye stars are drawn in an attrative style and with an unusual accuracy. The classical figures were still drawn in, but with less prominence than in the earlier atlases.
After that, together with a group of assistants, Argelander created a catalogue with the positions of 325,000 stars, down to approximately magnitude 9.5. All positions were measured from visual observations, and covered the sky from the North Celestial Pole to declination -2°. The positions from the catalog were used to create 37 large star maps. This monumental work became known as the Bonner Durchmusterung, and was first published in 1863 (figure 12).
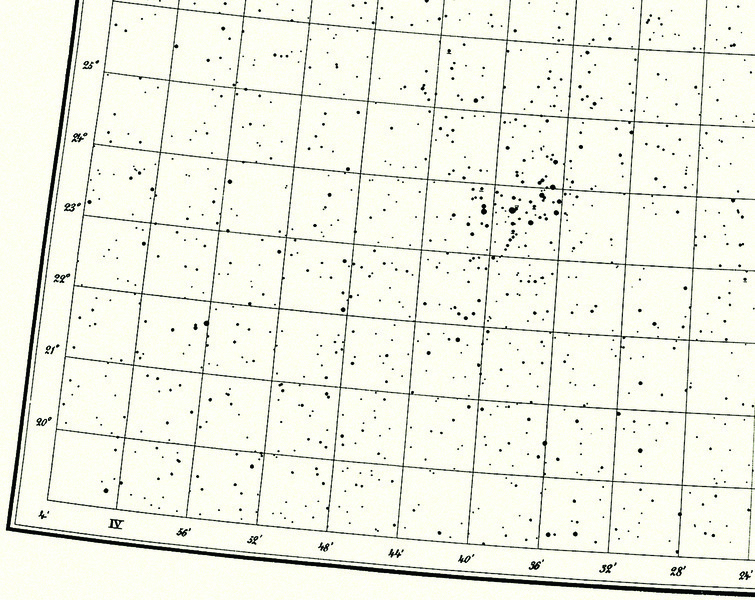
Figure 12. A detail from the Bonner Durchmusterung star charts. (Bonn, Germany, 1863). The chart shows part of the constellation Taurus, with the open star cluster the Pleiades.
After Argelander died in 1875, his work was continued to declination -23° by one of his assistants, Eduard Schönfeld. It became known as the Südliche Bonner Durchmusterung and was published in 1886. The final two parts of this work, the Cordoba Durchmusterung, were compiled in Córdoba, Agentina, and published in 1908 (to declination -62°) and in 1930 (to the South Celestial Pole).
Argelander’s work remained unsurpassed until the 1960s. Then a comparable work was published by the Smithsonian Astophysical Observatory, or the SAO, in four volumes, containing the accurate positions of about 260,000 stars. Using these positions, and using—for the first time—computer plotting techniques, 152 star charts were created; The SAO Star Atlas (figure 13).
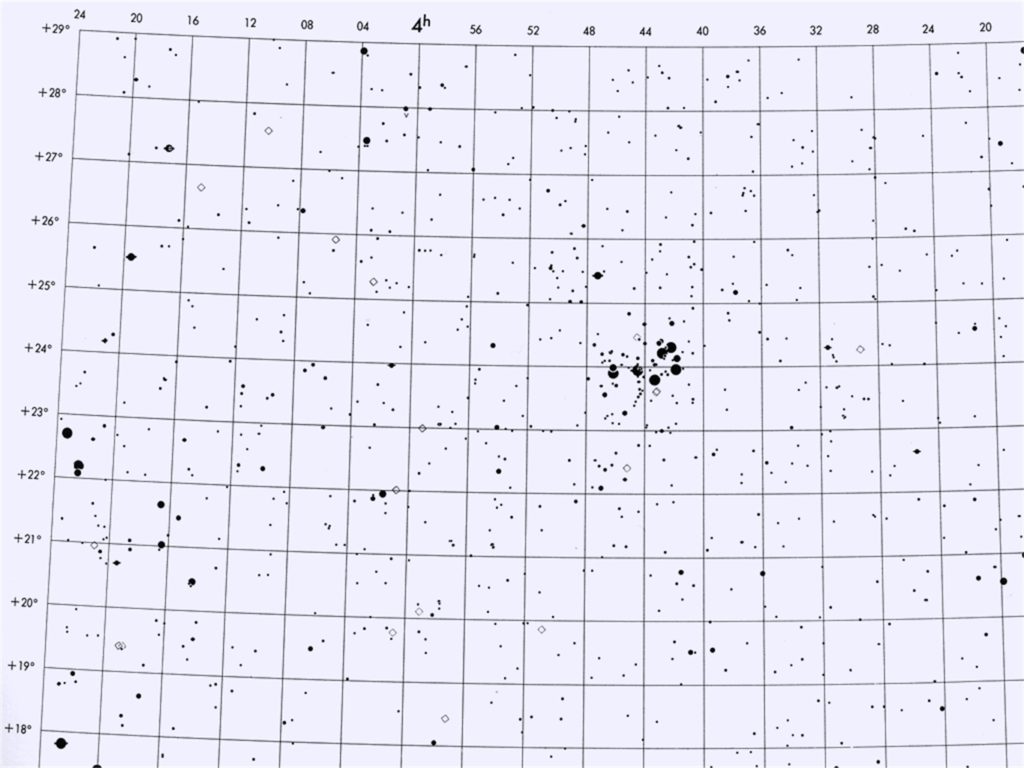
Figure 13. Detail of one of the charts of the SAO Star Atlas (S.A.O., 1969), also showing the Pleiades in Taurus.
There was nothing left of the beautiful artistic work of the old days. Looking at the maps of the SAO Star Atlas, you do not even see the names of those classical constellations.
During the last part of the 19th century and into the 20th century, another need arose. More and more star enthusiasts could afford to buy a small or medium size telescope, and for those amateur astronomers easy-to-use star atlases were needed to help them navigate the sky and find interesting objects.
But that is another story.
About the Author
Wil Tirion is a Dutch uranographer (celestial cartographer). His most famous work, Sky Atlas 2000.0, is renowned by astronomers for its accuracy and beauty. The second edition of his most complete work, Uranometria 2000.0, was published in 2001 by Willmann-Bell. He is also responsible for the sky charts found in many other publications. He was originally a graphic designer. The minor planet (asteroid) 4648 Tirion is named after him.



